NASA

SPACE SETTLEMENT CONTEST

 

 

TEBA 1

 

 

By

 

Horia Mihail TEODORESCU

Lucian Gabriel BAHRIN

(Small team, 8^th grade)

(small group 6-9 grade)

 

Under the supervision of:

 

Prof. Horia Nicolai Teodorescu

Prof. Adam Korilloff

Prof. Margareta Constantinescu

 

 

Romania

2003

 

Contents

 

Acknowledgments ....................................................................................................  iii

 

Preliminaries: An introduction: Requirements for the station ...............................  3

 

Chapter I How and where should we construct it?

     Who will build and inhabit it? How to start?....................................................... 5

By Horia Mihail Teodorescu and Lucian Bahrin

 

Chapter II Building the space station...................................................................... 15

By Horia Mihail Teodorescu

 

Chapter III: Creating the living conditions: atmosphere,  ecosystem, agriculture........... 19

By Lucian Bahrin

 

Chapter IV: Raw materials: Chemistry and Metallurgy Issues ...........................  23

By Lucian Bahrin

 

Chapter V: Electric energy and solar panels on the station ..................................  29

By Horia-Mihail Teodorescu

 

Chapter VI: Shielding against cosmic rays and solar flares ..................................  31

By Horia-Mihail Teodorescu

 

Chapter VII: Analyzing vibrations .......................................................................... 35

By Horia-Mihail Teodorescu

 

Chapter VIII: Chaotic vibrations ............................................................................ 45

By Horia Mihail Teodorescu

 

Chapter IX: Locating the space settlement ............................................................ 49

By Horia-Mihail Teodorescu

 

ANNEX..................................................................................................................... 55

By Horia Mihail Teodorescu

 

General References ................................................................................................. 57

 

 

We, Teodorescu Horia Mihail and Lucian Bahrin, have both cooperated in discussing the general plan of the research.

 

Acknowledgements

 

Our teachers who helped us with this project are:

 

Dr. Horia-Nicolai Teodorescu, a university professor and member of the Romanian Academy, who is my father and mentor (Horia-Mihail Teodorescu) and helped us with the incentive for this project, with references, and with most of the advising. He also corrected many of our errors.

Mr. Adam Koriloff, a physics professor at the high school “Colegiul Costache Negruzzi Iasi”.

Mrs. Margata Constantinescu, is a chemistry professor at the high school “Colegiul Costache Negruzzi Iasi”.

 

We thank them all for the help for this project. We also thank them for their oral communications in which they taught us.

 

Thank you for your attention.

 

We foremost thank God for allowing us to do our work for this paper.

 

 

PRELIMINARIES

 

An introduction: Requirements for the station

 

By Horia-Mihail Teodorescu

 

 

Requirements are features that a customer requests to be included in the design of a desired product. The station is also submitted to requirements.

 

We will first analyze what the Governments contributing (paying) for the station would require. We will search for their most probable interests in the space station.

The governments that contribute in building the station must be stable and great economical powers. Also they must be in political harmony and must be able to sustain the construction of the station with money constantly.

Their interests can vary from constant income from the station as products, or to control a part of the station. Their interests can vary also to political interests, like having an economical and political alliance with other governments that contribute to the construction of the station.

The station must be able to repay the governments that invested in it. Therefore, the station must be an international spaceport and a tourist location. Space tourists can be a good source of money. Also assembling spacecraft and satellites can become an important source of money. The fuel needed to bring the rockets or satellites up to the station can be spared. Building spacecraft and satellites in the space station can be a good way to earn money and repay the governments. Another way to repay the governments will be scientifically. Astronomers will inhabit the station and great research can be made. A telescope like Hubble placed on the station can bring great science income.

Another advantage will be doing experiments in space, in conditions of zero gravity and perfect vacuum.

 

Companies: Requirements, interests

 

The companies contributing for the station must be stable financial empires. An example would be Microsoft. Other powerful companies may want to contribute to the station’s construction. The interests are clear: earning a part of the station or a facility, or placing “shops” in the station. The companies may want rare materials extracted from the Moon’s surface, or have a part of the station solar panel and earn money from electric energy. Some companies may want to own a facility and earn money from scientific awards.

 

Scientists: experiments and research

 

Scientists may suggest experiments in using the perfect vacuum of space. Because on Earth there cannot be made such a perfect vacuum, some experiments cannot be done, like growing crystals in special conditions. Also, zero gravity can offer great alternatives: experiments can be made, experiments that are impossible on Earth. Some experiments are impossible on Earth due to its gravity and magnetic field.

Thus, the state of zero gravity can be used for some experiments and to determine how certain materials behave in such conditions. If the temperature is very low (), an effect of super conductible will appear. This effect is interesting to study. If we can reproduce that effect on Earth, we may be able to build faster microprocessors.

Studying the near galaxies is important for the astronomers from the station.

 

People: Wishes, requirements

 

The people would require reasonable living conditions. We have to ensure water, oxygen, light, gravity as basics for each person. The quantity of water and oxygen each person needs will be calculated. We will consider that we will reduce the quantity of nitrogen with ½ from the normal quantity on Earth. The pressure will be the same as in the high mountains.

Also, shielding has to be made so that the radiation is not more than 0.5 rems/year. Except for these major problems, a magnetic field to simulate Earth’s must be installed.

A requirement for of living space is needed. A total array per person will be of about 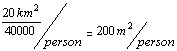 with streets, home, parks, working place included.

   

CHAPTER I

 

How and where should we construct it?

Who will build and inhabit it? How to start?

 

By Horia-Mihail Teodorescu and Lucian Bahrin

 

Construction phases. Population design for the construction phase

 

The construction of the space station will be in 2 phases:

·           Build a station for cheap material extraction from the Moon and ship ore to the station.

·           Build the station.

 

We decided that the Moon would be a major resource of metal, minerals, water, and construction material for the station. It is obvious that the major material resources of space are the planets, their moons and asteroids. The distance from these objects to the space station determines the accessibility to these resources.

The close planets of the solar system and the moons may become the major resource well near the station. However, planets are very distant from possible places where the first colonies could be built. Also, we have to know that planets have usually deep gravitational wells and that the effort of a rocket to leave a planet’s surface is very big. The Moons of planets offer better opportunities than the planets because moons have shallow gravity wells. Moons like those of Mars have very shallow gravity wells, but are too far away to be considered as useful. This argument applies to the other natural satellites of other planets.

Earth’s natural satellite, the Moon, offers a good choice. Near the space station, the Moon has a shallow gravity well () and offers a much better solution than transporting materials from Earth. Also, the Moon can be a very important source of aluminum, titanium and iron for constructing the space station and oxygen for respiration and fuel and frozen water. Earth may still be the station’s most important source of carbon and nitrogen that are in very small quantities elsewhere in the space.

We choose the torus for the construction of the station. The torus has the best expandability and is the easiest to construct of all the other variants (see figure I.1). A multiple banded torus is the best solution we have for expandability and life support.

 

Building stations and population design

 

Our station cannot survive without the material for construction. The best alternative is that the material should come form the Moon. If we will take material from Earth, the effort and cost is 22 times greater than taking materials from the Moon. Indeed, the spacecraft has to do a much larger effort to escape the deep gravitational well of Earth’s, but 22 times less effort to lift up the surface of the Moon. Asteroids offer very shallow gravitational wells, but are too far away and their regularity and hard to determine orbit leaves them no chance as a first choice. However, asteroids (when encountered) can offer enough material to build an entire space station. Comets are too far away and very rare and have a very irregular orbit. Also, comets have very shallow gravitational wells. They may offer a source of material for the colony.

Therefore, the Moon will be the major source of materials for the space station. Of course, even from the beginning of the construction of the space station, there has to be an extraction facility on the Moon to supply the construction. The construction of the Moon extraction station will be the first step that will have to start before beginning the construction of the space station itself. I made a scheme of the extraction facility (figure I.2).

The next table is about population design for the construction phase of the extraction facility. The personnel will come in time, after the living quarters were built.

 

Population Design for Moon Extraction Facility
Profession	Higher level professionals (design engineers, shift engineers)	Medium level professionals	Total number
Metallurgists	3	17	20
Metal Constructors, welders etc.	3	17	20
Miners	5	45	50
Mechanics experts	2	10	12
Electronics experts	2	10	12
Drivers	1	4	5
Chemists	5	0	5
Informatics program designers	2	3	5
Communications	2	3	5
Doctors	2	0	2
Biologists	2	0	2
Power plant maintenance personnel	4	0	4
Astronomers	2	0	2
Physicians	2	0	2
Agronomists	2	3	5
Alimentary industry	2	3	5
Administration	3	-	3
TOTAL NUMBER			164

 

Remark: After finishing the construction there will be no need for so many metallurgists and metal constructors and wielders. Therefore, many will move on the space station to continue building there. On the Moon extraction facility, only 10 metallurgists will remain and 5 metal constructors and wielders. Later, for the construction phase of the spaceport, additional workers will come, but this is not our problem.

After the first phase of the construction is complete, the construction of the space station can begin, after having a constant supply of materials from the extraction facility. I will now show a population design table for the construction phase of the station. (Of course, the personnel will come in time.)

 

Population Design for Space settlement
Profession	Higher level professionals (design engineers, shift engineers)	Medium level professionals	Total number
Metallurgists	10	90	100
Laminar	5	50	55
Metal Constructors, welders etc.	20	180	200
Resistance structure engineers	10	0	10
Mechanics experts	3	27	30
Electronics experts	5	50	55
Drivers	3	27	30
Rolling materials maintenance personnel	2	8	10
Informatics program designers	20	80	100
Communications	10	100	110
Medical personnel	10	15	25
Biologists	5	-	5
Thermo technicians	5	50	55
Hydro technicians	5	50	55
Automatist engineers	30	-	30
Agronomists	5	50	55
Alimentary industry	3	50	53
Leadingship	20	-	20
Chemists	10	100	110
TOTAL NUMBER			1108

 

Remark: The determined values are only for the construction phase.  After this, the rest of the colonists can come as the living quarters are constructed.

 

Political importance of the station (By Horia-Mihail Teodorescu)

 

Of course, the space station will need its leadership. We purpose a democratic kind of government. Democracy and a pyramid-based society would be the best kind of leadingship. Also, I have to analyze the political contest and the expense of building such a station. The expense of sending people into space is great: 1 billion $ per spaceship. Therefore, the expense of sending more than 10000 people into space will grow at many billions of dollars. With the actual type of spacecraft, only 7 people can be sent into space by spacecraft. We have to build much larger and sophisticated spaceships so that we can send more people into space on one single spacecraft. The project is about 100 people per spacecraft.

Because only the expense of sending so many people into space is so great, no country or state in the world can afford it alone. Therefore, the space station should be international and the costs supported by the alliance that builds it. Some political aspects are important and must be foreseen. First, this economical alliance that helps build the station is important not only in an economical view, but also in a deep political alliance. This can help extend NATO almost all over the democratic world with the states that participated in building the space station. Also, the space station is a guarantee for peace between the nations that built it. We can also think at an alliance between states around the world that could insure peace and political harmony on Earth. The importance of the project and the scale of the project means that it will involve not only the three states in the world that can build rockets and send people into space, but also the other states that will contribute with money and material to support the construction of the station.

 The states that supported the construction of the station economically or with spare parts will be in the alliance. The second important fact is that most of the states must be involved somehow, so that the alliance can grow and peace all over the world can be realized. But, the states that are not in this alliance can become enemies of the states that built this station. Therefore, there must be no political discrimination to the people send to the station to prevent a possible war.

 

Building the Moon Extraction Facility  (By Horia-Mihail Teodorescu)

 

Initially, before constructing the space station, we must build the Moon Extraction Facility that will supply the constructors with materials.

Initially, in the building of the Moon Extraction Facility the need is for a team that will construct a base with living quarters for the personnel. Also we will need additional personnel to build a “bucket propelling system” for sending materials with a low cost to the space station.

On the station we must begin the construction of the robotic arm that will catch the materials send from the “bucket propelling system”. In the beginning, only a net of a total area of will be built. The great expense of the robotic arm and difficult construction due to great mechanical complexity, this module will be the second solution. The net will be easily built and only a spacecraft to collect the shipped container will be needed. After the station is completely built, the net can be changed to the robotic arm.

Therefore, until the station is built, we choose the form of the passive catching system for the packages sent by the Moon Extraction Facility. A schematic design is presented in figure I.3.

Except for the personnel for the construction of the “bucket propelling system”, we also need personnel to build an atomic power plant of 25MW to supply the extraction facility with energy and supply the “bucket propelling system” with enough energy to supply the bucket propelling system to send packages to exit Moon’s surface and get to the space station. The atomic power plant will assure enough energy for the whole facility.

Because the Moon is only 50% of the time lightened by the Sun, using solar panels as an exclusive electric energy source is not a good idea. But the use of solar panels in the daytime to produce additional electric energy is not excluded. I have introduced the use of solar panels in my scheme (figure I.2).

Also, there will be always need for service personnel on the nuclear plant. Because the Moon hasn’t enough uranium, uranium will be imported from Earth. Because the nuclear plant only needs 50 kg of uranium to support the facility/yr, the cost is not very big.

 We chose the “bucket propelling system” because all the other alternatives are too expensive. If we had used the “gas propelling gun” as the NASA Summer Study proposes, the cost of the gas needed would have been too big to afford. Other solutions, like sending spacecraft with the material from the Earth, would have been too expensive and a spacecraft that can carry tons of material hasn’t been yet built and the costs would be great.

Water, , is found frozen on the Moon. The amount of frozen water on the Moon can partially supply the extraction facility and the space station for years, but water has to be recycled on the space station, because the amount of frozen on the water cannot supply 100% the station. The recycling of the water is presented in another chapter.

 

Other use of solar energy

 

·        Solar energy can be used for chemical reactions and for melting the minerals. Therefore, on the space station, metal should also be shipped, not only ore to be refined on the space station. This can significantly increase efficiency.

·        Also, the solar energy can be used on the extraction facility.

·        Moon buggies and trucks and extraction vehicles can use solar energy.

·        Electric metallurgy: Melting the metals in magnetic field is a very good alternative in melting metal in space and separating metal from ore. Instead of melting the metal with coal, like a traditional method, we can melt the metal in space with the help of electric energy. Another variant in melting the metals would be using an electric arc to heat and then melt the metal from the ore. The electric energy needed can be assured by the energy surplus made by the solar panels presented in figure II.1. Also, we can use the diverse metals melted from the ore at the surface of the Moon to create special alloy. Therefore, pieces and parts can be shipped already made on the Moon, made out of alloy prepared in the refinery.

 

 

Population design for the complete space settlement

 

Now we will discuss about the population design (in percentage for the space settlement and in values for the Moon Extraction Facility) after the construction period has ended and the space settlement is at its full capacity.

 

 

Resources for starting the space settlements construction (By Horia-Mihail Teodorescu)

 

In this Section we discuss problems like how shall we start building the space settlement and what are the resources needed to complete building the space settlement. We will discuss about the human, material and energy resources needed to build the space settlement.

First we have to analyze how much energy we need to launch the first module. An important fact has to be taken into consideration: both space settlements have to be constructed in parallel. This means that we have to construct the Moon Extraction Facility in parallel with the space station so that the materials needed for the construction are extracted and shipped in time for the construction process.

We will have to send two rockets, both in the same time, one to the L5 point where the station has to be constructed and one to the Moon to build the extraction facility.

We will need special rockets for such a task. We will calculate the minimum weight per rocket for the first module (the same values apply to the extraction facility).

 

Rocket load for module launch
Load type	Weight
100 people for an average weight of 80kg/person	8t
Food, water etc.	8t
Seed, growth chemicals etc.	1t
Tools	4t
Materials	5t
Total “useful” weight	26t
Base module	30t
Rocket and fuel	500t
Total Weight/Rocket	556t

 

As known, the rocket + fuel will weight about 10 times the total weight of the cargo. Therefore, much larger rockets must be built to achieve such a goal as sending 100 people into space in only one rocket.

Even with such a huge rocket, we will need about 100 rockets to complete the space station with a total population of 10000. Also we will need another 2 rockets to complete the Moon Extraction Facility.

We will now calculate the energy needed to get the rocket up to the L5 point. The distance up to L5 point is used in the following calculus: , where L is the mechanic work, F the force, d the distance.

We know that on Earth the following formula is available for potential energy:

 

,

 

but the formula applies only if , which is false in our case, because up to the L5 point  is variable with the altitude. In our case, the following formula applies:

 

,

 

where M is the mass of the Earth, m the mass of the rocket, R the distance between them and k the universal constant:

 

Therefore, we will have the following formula for the mechanic work:

 

This allows us to do the computation of the energy needed to launch the rockets.

 

Volume, total surface array and mass computation

 

We now estimate the global dimensions of the space settlement. We know that, for a torus:

 

We will consider that the major radius, R, and the minor radius, r, have the following values:

 

  

 

Then, the total volume is:

 

(In the computations, we approximate .)

 

The total surface array is:

 

 

The total mass of the space settlement is . (This value is from: http://www.nas.nasa.gov/NAS/SpaceSettlement/75SummerStudy/)

 

 

References

We have read several materials on NASA Space Settlement Contest site (see the final Reference Section) and we answered several questionnaires Prof. H.N. Teodorescu forwarded to us, regarding these general issues. Discussions with Prof. H.N. Teodorescu have been instrumental.

 

 

 

Figure I. 1

This figure shows that the construction of the torus can be made easily in a module adding construction. We begin with one module and then we extend to the whole torus.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Figure I.2

This figure shows that the construction of the spacestation begins in modules. The first module in the first cylinder. After this, more modules add to the structure, as showed in this figure.

 

 

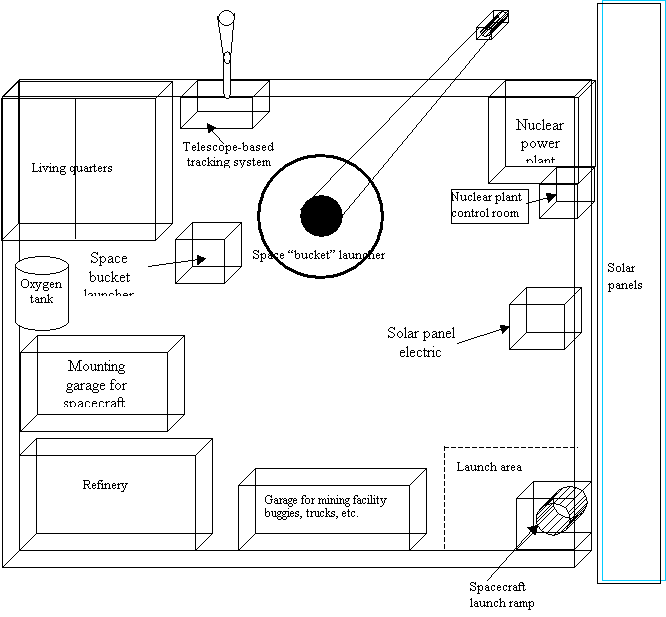
Figure I.3

Figure I.3 represents a scheme of the extraction facility on the Moon

 

 

 

 

 

 

Chapter II

 

Building the space station

 

By Horia-Mihail Teodorescu

 

 

We saw in Chapter I that the space station has to be built in parallel with the station on the Moon. We understand that the station has to get materials from the Moon extraction station. We also understand that this two projects must go constructed I n parallel, because the bigger the need for the materials from the station gets, the bigger the Moon Extraction Facility will get.

We discussed in the previous chapter about two steps in population design:

 

1.                       The construction phase, in which both the stations will have a start in the number of people (workers, constructors) for the building of the station. All the inhabitants will work in building and developing the stations and all the inhabitants are mature young people.

2.                       The construction phase over, the living stage, when all the 10000 supposed inhabitants of the space station will come to the station. This is assumed as a final population and the population design in the final stage, for both the stations, is assumed in the next chapter.

In both phases, the space station has to sustain itself. We will now start with the building procedure.

We will first send two rockets into space. The construction is supposed to be a pyramidal construction. We will begin with a cylinder for living quarters of the 5 astronauts that will begin the construction of the space station. The other rocket will go on the Moon to start constructing the extraction facility. The second rocket will contain small docking living station and a moon extraction buggy.

The space station’s construction begins with a cylindrical module for the living quarters of the builders. Even from the beginning the space station must be able to self sustain itself, therefore it must be able to produce food and recycle water oxygen to sustain life. After the first stage is completed, the other modules can be put in place. We thought that at the beginning a structure made from two cylinders tied with two communications tubes to a rotation center structure would be the best alternative. The rotation center structure can be the spaceport. After this structure is complete, we can continue in building the whole structure of the torus by adding modules. The parts can come already in shape from the extraction facility to increase the speed of the construction. As it concerns, the torus will be made of many such parts, so it will almost be round. Building round parts/shapes in space is very difficult, so we thought that using block-shapes would be much easier. Of course, the choice remains to the constructor and the funds available for the construction (using round shapes would mean further expense).

It is known that we cannot suspend the station motionless in space, because to stay up and resist gravity, the station must move always with a constant angular speed to follow its orbit and not crash down. We found an interesting method in maintaining the station into orbit. Instead of using conventional rocket-propelling engines, we shall use a less expensive and much more fable propelling system. The station has to rotate to maintain its orbit. Also, , the angular speed, must be constant. To make the station rotate, we need a momentum of forces. Two engines can sustain this momentum. We found a much more economical solution to the problem. Using rocket-propellers would mean huge costs in fuel. Using conventional gas thrusters would also mean enormous costs.

The only energy that is really abundant is the solar energy. We can use solar panels to provide the station with its electric energy, but also to propel the station[1]. By using on one side a solar sail, we can obtain one of the forces of the couple with no expense. Solar sails rely on the pressure of the sunlight. That pressure is the one exercised by the photons and by the solar wind on the sail. This force is enough to move slowly the station in the needed direction if the sail has a surface big enough.

In space, the pressure made by the sunlight (included the solar wind of particles) is powerful enough to supply one of the forces in the momentum. The solar sail should be able to move and change its direction so that always the sunlight can fall directly on the surface, at an  angle.

The sheet must be able to move into several directions. A robotic arm for it to move such as always the Suns rays will be able to fall at an  angle must ensure this ability, like in the Figure II.1. Also, the robotic arm must be positioned on a rail system so that it can move around the torus and provide it with the force of an opposite sense with the force given by an engine at the other side. Because we cannot rotate the station by positioning two sails, we must put an engine to do the job of the other force in the momentum. The robotic arm must have an anchoring point with a small engine to move the sail around the torus to be sure that the solar rays fall at a 90⁰ angle on the surface of the sheet.

  An engine means further expense. Also we need fuel for the engine that must be imported from Earth. We cannot afford a rocket engine because of its expense. The best solution in this case is an ionic engine[2] to do the job of the second force in the momentum of forces that rotate the station to create gravity. An ionic engine is cheap and needs very little quantities of fuel to work. An ionic engine is the best alternative and it can be the one to do the job.

The active propellers, the ion thruster, will develop a constant thrust of ions to keep the station in its orbit. The momentum of forces must maintain the constant rotation of the station.

The ion thruster provides enough thrust to be one of the forces in the momentum. An ion thruster has already been tested, at NASA’s JPL in 1996. As NASA officials say, the ion engine is a more efficient propeller in space. Xenon, a heavy inert gas, is the right fuel for an ion engine.

Ion thrusters are more efficient than rocket engines in space, because ion thrusters expel molecules from the engine at a higher speed. An estimated ion propulsion exhaust speed is 70200 miles per hour.

Chemical propellers have an exhaust velocity of only 10400 miles per hour and consume much more fuel than an ion thruster.

The thrust from an ion engine comes from accelerating and expelling positively charged ion atoms. The estimated power needed for the ion thruster is 2000 watts.

We will now compute the total solar panel array needed for the ion thruster.

The solar constant (Solar energy flux per ) is . We estimate that the efficiency of the solar panel is . Therefore, the solar panel array that required powering the thruster would be:

of solar panel array to power the ion thruster.

The atoms are expelled from the thruster in a great number and at a velocity of about 70200 miles per hour. Although, the accumulative mass is so low, it will provide enough thrust at first to rotate the station with a few mm/s.

Because in space there is no friction, the rotation speed will have a constant acceleration up to the desired velocity value. This will provide a final rotation speed close to that of the Earth, of about . We think to arrange a system using ion thrusters and a solar sail for the rotation of the station that will assume a gravity role.

 

 

 

Figure II.1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

CHAPTER III

 

Creating the living conditions: atmosphere, ecosystem, agriculture

 

By Lucian Bahrin

 

Basic Space Agriculture

 

          Astronauts will have to leave Earth with enough food for about 2 months. But once in orbit or on the Moon, they will have to start to produce their own food. At first, they will grow plants like Salad (which grows very fast). We do not exclude the possibility of growing genetic modified plants, so that they will grow faster and in some cases, occupy less space]. These will be the basic of their alimentation. Then, they will have to grow wheat, potatoes, soy, corn, etc. After 2-3 cultures they will have to rotate, so that the soil will be protected. Later on, animals will be a part of this process too.

            But until animals will be grown, plants will be the only source of food available on the two Space Stations. Humans need proteins to develop normally. However, plants are not so rich in proteins. Only a few types of plants, like Soya and Beans, provide enough proteins. Therefore, these plants will be in the everyday menu.

 

Advanced Space Agriculture

 

            Once the Space Stations are finished, we can start growing animals and other types of plants. We can even build special rooms where we can create small “forests” with small ponds, fur-trees and wild animals, like deer or wild boars. We don’t need predators, because the ones on the Space Stations will consume this animal’s meat. Of course we will grow domestic animals, too. This way, animals will become a part of the every day diet. We can also build aquariums in which to grow fish for food or even pleasure. Special designed rooms will host trees whose fruit can be eaten. These trees will adapt to the climate on the Space Stations in time and they will start producing more fruit if they will be carefully taken care of.

 

Atmosphere

 

The atmosphere should be similar to the one on the Earth, namely 78% nitrogen, 21% oxygen, 0.03% carbon dioxide and 0.07% other gases. Thus, when the first modules leave Earth, they will have to be full of air. However, on Earth, at higher altitudes, the pressure is lower and the air becomes more rarified. If humans can survive with less air than the one at the sea level, we can modify the atmosphere on the Space Stations. So, if we do not have enough nitrogen for example, we could use helium instead.

 

Maintaining the atmosphere

 

            Once in orbit, the space modules will have to maintain their atmosphere. For this, we have to create a whole ecosystem, special designed for the beginning of the Space Station.

When we breathe, we inspire oxygen and expire carbon dioxide. Plants, on daytime, inspire carbon dioxide and expire oxygen. This is what we call Photosynthesis. But when there is no light, photosynthesis cannot take place. Still, the plant must breathe. That’s why, in the dark, plants inspire oxygen and expire carbon dioxide. Fortunately, the carbon dioxide expired during the night is less than the oxygen expired during the day.

That is why, on our Space Station, the day will last 15 hours and the night will last 9 hours. This way, we will be able to create the oxygen that we need.

We can also obtain oxygen from metal oxides. If we mine for metals and we find oxides, by heating them, the oxygen gets separated from the metal.

Another problem is the humidity of the atmosphere. The Space Station will require air conditioning systems, so that the humidity will be normal and the temperature will be about 20 degrees Centigrade.

 

Creating a new atmosphere

 

Only the first two modules will be filled with air when they leave Earth. So, when the rest of the Space Station is completed, it will need atmosphere. The already existing atmosphere won’t be enough, so we will have to find a solution.

Supposing oxygen won’t be a problem (it can be extracted from metal oxides found on the Moon), we still need a source of nitrogen and carbon. ß Illmenite.

 

Plants

 

            Beside the plants the astronauts will have to grow for food, other plants will be needed. But plants also require space and soil. It won’t be easy to bring soil from Earth or Moon. Therefore, we could use plants that do not need roots. These kinds of plants grow in some parts of the world like Spain even on telephone wires. They take everything they need from the air. Of course, certain humidity will be needed for this. But this will not be such a great problem. After all, there won’t have to be only these kinds of plants. We can and we will grow soil plants. At first, soil will have to be carried from Earth. But then we can use lunar soil, after we fertilize it.

 

Water

 

Water is one of the most important elements of life. When the first space modules will leave Earth, they will have to carry water supplies. We cannot find water in space; recycling the existent water will be the only chance of surviving. Using different chemical substances (these substances will be created on the Space Station and on the Moon Station) we will be able to purify urine. During the purification process, we will also obtain salt and other substances that will be later on used in different chemical processes. We also mustn’t forget that humans and plants eliminate water through perspiration. This water will have to be rescued and purified.

We could also build small aquariums in which to grow fish and other animals for food.

Water can also be extracted from the moon. On the Moon Station, besides recycling the existent water, we will mine for it and then purify it. Then we can transport a part of it to the Space Station.

Comets represent another source of water. Though comets are very rare and we cannot land on a comet in our times, we mustn’t exclude the idea that somewhere in the future we could use comets to extract water.

 

Diseases

 

            Drugs will be a problem, at least for the first few (3-6) months. Therefore, a sterile environment will have to be created. Air, soil, constructing materials, they will all have to be sterile. Plants and humans will all be carefully selected, so that no microbes are carried on the Space Stations. These drastic measures (drastic indeed) will have to be taken only until we will be able to produce drugs. Why drastic? Because, be creating a perfect sterile environment, we damage (slowly but sure) the human immunity system. With no microbes to fight, the human body will produce fewer antibodies. This would be a disaster if a simple disease like Common Cold gets on one of the Space Stations.

            So, when the first drugs will be made on the Space Stations, harmless microbes will be released into the atmosphere and after a while, other microbes that cause diseases like cold.

            We do realize that once released, the microbes will start multiplying. They will also evolve in a different way than on Earth. But people on the Space Stations will also evolve different. In time, their bodies will adapt to the life in space. Once with the birth of the first generation of children in space, we might say that a new race has been born. These children will easily adapt to life on the Space Stations.

            Though we will try to create conditions similar to the ones on Earth, we will not allow people that carry viruses like HIV or other dangerous microbes on the Space Stations. Diseases that could cause death will be destroyed before they can reach the launching station.

 

CHAPTER IV

 

Raw materials: Chemistry and Metallurgy Issues

 

By Lucian Bahrin

 

Mining the Moon

 

            Once we have a space station on the Moon, we must start mining for raw materials. For this we will need special designed vehicles, using electricity as a source of power. At first we will not be able to use explosives, because we won’t have what it takes to produce them. That’s why we will use huge drills to extract minerals. Once on the surface of the Moon, the minerals will be loaded into transport vehicles and taken back to the Moon Station.

            Here we will need to separate the elements and then produce different materials that will be used in constructing and expanding the two Space Stations.

            A very important metal that we will need is Titanium. This is found on the Moon in Titanium dioxide. Here are the reactions we will use to separate Titanium from Oxygen:

                        CaCl2 à Ca + Cl2 (using electrolysis)      [Bhogeswara Rao et al]

                        2Ca + TiO2 à Ti + 2CaO                         [Bhogeswara Rao et al]

            The first reaction takes place when the calcium chloride is melted. The electrolysis device is described in Fig. 1:

                                                                                       Cl2

 

 

 

 

 

 

 

 

 

 

 

 

                                                             +         -

 

                                                    Fig. 1

           

The second reaction takes place at high temperatures. The calcium oxide is lighter and will rise at the surface. Titanium is a heavier than calcium oxide and will go to the bottom of the tank, where it will be collected. It can then be used in different alloys for constructing the Space Stations. The Titanium plant is described in Fig. 2:

 

           

                              

                                                           

 

 

 

 

 

 

 

 

                                                                                                                                                                                                                                                                                                                                                                                                                       

 

                                                               +         -        

 

 

Fig. 2

 

                                                                                                                       

            Another important element is Aluminum. We will present the topic heavily citing and borrowing from the paper by [D. BHOGESWARA RAO et al], quoted in the references. “The main source of aluminum in the lunar soil is plagioclase concentrate which contains mainly anorthite, (Ca, Na)(Al,Si)4O8-on Earth, aluminum is not normally produced from anorthite, although such resources are being seriously considered because of depleted supplies of bauxite ores.  The major difference between anorthite and other minerals is the calcium content, which might prove to be a considerable problem in the extraction of aluminum.” [D. BHOGESWARA RAO et al]

            The soda-lime sintering process is the only one known on Earth. The Bureau of Mine developed it and it was tested by pilot plant operation and in laboratory. Here is the general reaction of the process.

 

CaAl2Si2O8(s)=3CaCO3(s)+Na2CO3(s) à 2NaAlO2(s)=2Ca2SiO4(s)+4CO2(g)    (1)

 

            The products will be treated to obtain alumina. Large amounts of sodium and calcium carbonates will be needed, because each mole of anorthite consumes 1 mole of Na2CO3 and 3 moles of CaCO3. These materials are not to be found on the Moon. This process also requires large amounts of water. Therefore, we will need another solution.

            Out of aluminum monohalide process, carbothermic reduction, electrolysis and carbochlorination, the chosen ones were carbochlorination, followed by electrolysis of chlorides. “In Carbothermic reduction, the oxide reacts with carbon to produce metal and carbon monoxide:” [D. BHOGESWARA RAO et al]

           

            MxOy(s)+yC(s)à xM(s, l)+yCO(g)     (2)

 

            Because the constituent oxides of anorthite are stable, we will need very high temperatures (2500 K). Other compounds such as SiC, Al4C3,Al4O4C (condensed phase) and Al2O, SiO, Al, Si and Ca (gaseous phase) are invariably present at these temperatures. These phases make a type (2) reaction very complicated. The complications in carbothermic reduction of alumina were recently explained by Grjotheim et al. In carbothermic reaction, metal losses occur because of the substantial vapor pressures of  Al2O and Al. “Gitlesen et al. calculated the partial pressures of Al, Al2O and CO in the-system Al4O4C-Al4C3-Al, where Al4O4C and Al4C3 are the condensed phases formed during the carbothermic reduction of alumina. It is fairly conclusive from their calculations that the aluminum and aluminum-sub oxides pressures are, so high below 1900^o C that liquid aluminum cannot be formed at normal operating pressures.” [D. BHOGESWARA RAO et al]. The following reactions would consume any liquid aluminum added to the system

           

            Al4O4C(s)+2Al(l)à3Al2O(g)+CO(g)  (3)

           

            Al(l)àAl(g)      (4)

 

In this way, that the equilibrium compositions of the gas phase would be maintained. At temperatures above 2100^o C, solid aluminum carbide decomposes to aluminum and carbon. Favoring the formation of aluminum, carbon-monoxide partial pressure increases rapidly with respect to Al and Al2O. Still, unless special conditions are maintained, metal losses would still be significant.

 

Carbochlorination Methods

 

            Therefore, “a low-temperature carbochlorination with Cl2 followed by an electrolysis of the aluminum chloride produced appears to be promising”. [D. BHOGESWARA RAO et al] We must first consider a carbochlorination method using AlCl3.

High-temperatures carbochlorination with AlCl3- In this process, aluminum mono chloride is shock-quenched to obtain Al. The process is represented by:

(5)

Al2O3(s)+3C(s)

+AlCl3(g)-T=1800Cà 3AlCl(g)

+3CO(g)-Shock Quenchà2Al(l)+AlCl3

 

Many problems will arise when this process will be used to extract Al from anorthite. Much higher temperatures will be needed to obtain a reasonable yield of AlCl, because of the reduced activity of alumina. Severe problems (corrosion of the reactor material, for example) would be posed by this high-temperature process. Further, because of the substantial amounts of SiCl2 and CaCl2 present in the vapor phase, we would obtain an alloy that contains Ca and Si, which would then require an additional purification step. Besides, this process is not so sure, because it was only tested on a bench scale.

Low-temperature carbochlorination with Cl2- In this process, AlCl3 is reduced to aluminum by manganese (at about 250C). AlCl3 is obtained from ores that contain alumina.

“Previous studies of low-temperature carbochlorination of ores that contain alumina have been mainly confined to bauxite and clays which are essentially CaO-free. Anorthite contains significant amounts of CaO, and any chlorination process for anorthite must consider the formation of highly stable CaCl2. Fortunately, CaCl2 is a very useful by-product of the carbochlorination of anorthite”. [D. BHOGESWARA RAO et al]

Here are the reactions that are to be considered in the thermodynamic analysis of this process.

 

(6)        Al2O3(s)+3C(s)+Cl2à2AlCl3(g)+3CO(g)

 

(7)        CaO(s)+C(s)+Cl2(g)àCaCl2(s)+CO(g)

 

(8)        SiO2(s)+2C(s)+2Cl2(g)àSiCl4(s)+2CO(g)

 

The net reaction is

(9)        CaO-Al2O3-2SiO2(s)+8Cl2(g) à CaCl2(s)+2AlCl3(g)+SiCl4(g)+8CO(g)

 

The preferable temperature for anorthite chlorination is between 675-770C.

­ Alkali, alkaline earth oxides, as well as FeO, MgO and TiO2 are present as impurities in lunar plagioclase concentrate. Therefore, we must consider chlorination reactions involving these oxides. The resulting chlorides are volatile and condensed with AlCl3. Vapor phase contains very little CaCl2 or AlCl3-CaCl2-FeCl2.If the required amounts of SiCl4 are used along with Cl2, the chlorination of SiO2 in anorthite can be prevented. This way we can use SiO2 for glass. By successive condensations we can recover AlCl3. FeCl3 (gas phase) is cooled to about 225 C to obtain it solid. In a second stage, AlCl2 and chlorides (except SiCl4 and TiCl4) are condensed at 90C, while in a subsequent stage at –30C we recover the latter. By centrifuging we can separate CaCl2 (liquefied by heating the reactor residue above 775C) form SiO2-rich residue. “The estimated composition of the residue should contain at least 75-82 weight percent SiO2 and no more than 5-10 weight percent Al₂O₃ and 10-15 weight percent CaO.” [D. BHOGESWARA RAO et al]We should determine the exact composition of the residue from actual experiments. With the hydrolysis of CaCl2 followed by calcination  we will obtain pure CaO.

 

Alcoa Electrolysis Process

 

The best process of obtaining Al from AlCl3 using electrolysis the one developed by Alcoa. Because of the fact that Alcoa solved most of the problems encountered in electrolysis and a plant producing Al from AlCl3 obtained by carbochlorination is in operation, we selected this method. This process has some advantages over the one developed by Hall-Heroult: it requires lower temperatures, it needs high current densities, carbon anodes will not be consumed and a much smaller working area is needed. The electrical energy this process needs is only 70 percent of the one used in the Hall-Herlout process.

“Because the technical details of the process are proprietary, only a brief outline and a discussion are given here. The feed consists of 3-10 weight percent of purified AlCl3 along with the required amount of alkali and alkaline earth chlorides”. [D. BHOGESWARA RAO et al]. Electrolysis takes place under inert conditions in a sealed cell made out of 20-30 bipolar carbon electrodes stacked vertically at a distance of about 1 cm. Every electrode acts like a cathode on its top and as an anode on its bottom. All electrodes, during normal operation, remain immersed in the electrolyte at a of 700^o C30^o C (operating temperature). The Alcoa process uses a current density of 0.8-2.3 A/cm² and a single-cell voltage of 2.7 V. Here are two typical compositions (in weight percent) of the electrolyte: “AlCl3(5), NaCl(53), LiCl(40), MgLi2(0.5), KCl(0.5), and CaCl2(1); and AlCl3(52), NaCl(53), and LiCl(422)”. [D. BHOGESWARA RAO et al] We must be carefully control the aluminum chloride concentration to make sure we will have a trouble-free operation. To prevent the discharge of alkali ions (as they form interchelation compounds with graphite, they become detrimental to the electrodes), we must maintain  the AlCl3 concentration above a certain limit. The high pressure of AlCl3 sets an upper limit. Also, to prevent anode consumption, the oxide content must be as low as possible. With an oxide content of the electrolyte below 0.03 weight percent, the electrodes should have an operating life of nearly 3 years. The cell has an energy consumption of 9 kWhr/kg of aluminum produced.

 

References

 

This chapter has been written mainly based on the article:

D. BHOGESWARA RAO, U.V. CHOUNDRY, T.E. ERSTFELD, R.J. WILLIAMS AND Y.A. YANG, Extraction Processes for the Production of Aluminum, Titanium, Iron, Magnesium, and Oxygen for Nonterrestrial Sources, http://lifesci3.arc.nasa.gov/SpaceSettlement/spaceres/V-5.html

 

 

 

 

Chapter V

 

Electric energy and solar panels on the station

 

By Horia-Mihail Teodorescu

 

 

In this chapter we compute the amount of energy needed from the solar panels. We have to determine a minimum solar panel area to insure the amount of electric energy needed for the station to work. After this, we will compute the amount of energy needed for the station to work with some industrial facilities and other needs like manufacturing goods, building spacecraft, energy needed for the robotic arms that catches the packages sent from the Moon and other needs.

We will first use the following values as a standard for an average consumption:

 

·                             An energy bulb uses in average 60W.

·                             For a computer 350W are needed.

·                             For a small electric motor, like in the vacuum cleaner, an average of 2000 W is needed.

·                             For a TV set, an average of 1000W is needed.

·                             For a motor in the refrigerator, 500W to 1000W are needed.

·                             For a motor on a trolley bus 200kW to 300kW are needed.

 

We will now determine the energy a human uses per day. It comprises energy used in home and energy needed for transportation and in school, work etc., plus the energy needed to manufacture the goods you use. This amount of electric energy needed to manufacture the goods we use is about 3% the cost of electric energy.

In home, the electric energy consumption is around 2450Wh by adding one TV, one computer, one refrigerator and 10 electric bulbs. In an average day, consumption is about 24.5kWh/day.

In transportation, it is around 200Wh and 0.5kWh/day, by estimating that about 1000 persons travel /day with a trolley bus, or a similar transportation need.

In school/workplace, electric energy consumption is about 1000Wh and about 1kWh/day, assuming that it is an intellectual job, and that 1 computer and other apparatus or 2 computers work and have 5 light bulbs working.

Assuming the needed energy per day per people on the station is about 10kWh, the total energy per day is about 35 kWh.

Consequently, the power needed per person is 2kW, with a maximum “crest” or “peak” power twice that much which is 4kW. Therefore, the “installed power”, needed for the solar panels, is 40000 kW, for 10,000 people.

We know that the solar constant, solar energy flux per m² is (formula obtained from http://lifesci3.arc.nasa.gov/SpaceSettlement/designer/tables.html)

With an “installed power” of 40000kW we will need:

 For is the minimum value. Thinking that this value is only theoretical, we can approximate (with no other important power consumers) that we need a minimum array . But this minimum array is obtained only if the efficiency of the solar panels is , which is a value only for ideal solar panels. “Ideal” is not our case. If we think that the efficiency of the solar panels is , then, we obtain:

 

 

 

This is a minimum solar panel array for minimum power consumption. But, we thought that we might use some industrial facilities on the space station, so we must include some electric power to supply the facilities. We will add for industrial needs for a 10000 people station a minimum array of another . The obtained value is:

 

 

Further calculus shows that we have to add some power used by the station in some of its most obvious functions. We will add the power consumed by the robotic arm that catches the packages sent from the Moon Extraction Facility, the energy needed for the ventilation system and heating, moreover the energy for the ionic engine we have to add another . Energy for the active shielding (if used) hasn’t been added to this formula. We will discuss this problem in the shielding chapter. Heating must be made electrically, because we cannot use other traditional methods (we don’t have coal or petrol to use in space).

The formula is:

 

 

This value is the minimal value to keep the station working in minimal conditions. This computation doesn’t include shielding, which may be active, i.e., electromagnetic. Further details on the shielding problem are presented in another Chapter.

Notice that with this area of the solar panel, there is no income from the exported electrical energy to the Earth. Income can come from electric energy if a larger solar panel array is used. Also, this value is for the built station of 10,000 people only. Using the same algorithm we can do further calculus for larger stations.

 

References

 

1. http://lifesci3.arc.nasa.gov/SpaceSettlement/designer/tables.html

2. Discussions with my father

 

 

 

 

Chapter VI

 

 Shielding against cosmic rays and solar flares

 

By Horia-Mihail Teodorescu

 

Shielding the station against cosmic rays and solar flare radiation is a major problem in the station’s design. We have to choose between passive and active shielding.

Passive shielding requires a large quantity of material. Passive shielding is known to work. We are protected on Earth by the atmosphere against cosmic radiation. The atmosphere is a passive shield against cosmic radiation. The Earth atmosphere supplies approximately of mass shielding. This shielding is very effective.

On the space station we shall simulate the conditions on Earth.  For our station we will need of mass shielding to keep the dosage of irradiation between .

 

Analysis of possibilities

 

Passive shield [1]

 

To offer a good protection we need to surround the colony with this mass shield. We will need many millions of tons of matter to be mined and shipped to the station.

For a space station complex of 7-banded torus with 4 components we will have 9.7 Mt of mass shielding. a single torus, we will need about  of mass shielding. Although mass shielding is very effective and it is known to work, it is not the best solution. Only the cost of this massive shield would be great. The time needed to mine so much material from the Moon is also very long.

We decide that the passive shield may be not the best choice in shielding. We will probably choose an active shield.

 

Active shield [2]

 

With this method we may protect efficiently against cosmic radiation. Plasma radiation shields may do the job of an active shield. Active shielding continually needs power to maintain our shield active. For an active plasma shield we will constantly need fuel (gas, we choose hydrogen) and electric energy to heat the gas such that it becomes ionized.

Plasma is a heated gas at high temperatures, like and is a flux of electrons and protons, if H2 is used, or ions and electrons for other elements. The gas is made of ions. If we use plasma as an active shield against cosmic radiations, we may reduce the radiation down to less than . We can disperse plasma all over the station and the flux of electrons and protons will electro statically repel or absorb the particles of the solar wind and the solar flares. The plasma may also repel the cosmic ray particles by its magnetic field.

We must heat the gas electrically. The electric energy needed for the plasma will be provided by the solar panels. We will need a supplementary layer for the station. In this layer we will have the gas heaters, the gas tanks and the generators. An additional control room for the plasma shield will also be needed.

We need to hold the metallic habitat at a positive potential of 15 billion volts. The enormous electrostatic potential repels the particles of the cosmic radiation. Another alternative is to use electromagnets to repel the particles of the cosmic rays. This electromagnet must be powered by about 15 billion volts to offer an even moderate shielding. The enormous consumption of energy shows us that this is not a good alternative. We will have to build a nuclear plant to power it up.

Next we have the design for the active plasma shield. Figure VI.1 shows how we built the station so that there is an external layer that includes the plasma shield modules. In this layer we find the gas tanks, the gas heaters and the plasma expellers. The next layer is the thermal isolation layer.

Figure VI.2 shows a diagram of the plasma system. We can see the gas, the heater, the communications tube and the expeller. We placed electromagnets in the tube to accelerate the particles. The plasma shielding system will give a very good protection to the space settlement’s inhabitants.

 

References

[1] NASA Space Settlement Summer Study:

http://www.nas.nasa.gov/NAS/SpaceSettlement/75SummerStudy/C…

[2] Plasma Core Shield:

http://www.nas.nasa.gov/NAS/SpaceSettlement/75SummerStudy/4…

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Figure VI.1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Figure VI.2

 

 

 

 

Chapter VII

 

Analyzing vibrations

 

By Horia-Mihail Teodorescu

 

 

In this Chapter, we analyze vibrations induced in the torus structure by changes of temperature due to the Suns rays heating.

We will begin analyzing the vibrations by analyzing how the Sun rays influence the temperature of the torus. Only a part of the torus is exposed to the Sun rays. The exposed part is expanding, while the unexposed part, plunged into darkness, contracts. We will approximate that 50% of the torus is expanding due to exposure to the Suns rays, while 50% is contracting.

We will first calculate the volume of the torus, based on the Figure VII.1 that illustrates the minor radius, r and the major rotation radius, R. The formula is . We use this formula in the computation to determine the expansion of the torus. We understand that an expansion force occurs to expand the exposed part of the torus. The force that contracts the unexposed part of the torus is equal to the force that expands the exposed part of the torus. We assume that the temperature for the exposed part rises up to  and the temperature for the unexposed part is about .

 Because the interior of the torus must be at a normal temperature of , we design the torus to have a thermal shield layer that keeps the temperature inside at the desired value.

Figure VII.2 illustrates the temperatures in the exposed part, the unexposed part and the scheme of the torus with the thermal shield layer.

 

We now begin the calculus with some basic laws:

 

, where  is the coefficient of linear expansion, is the initial length and and is the value for the temperature.

, where  is the coefficient for surface expansion, , S is the surface, is the initial surface and and is the value for the temperature.

, where  is the coefficient for volume expansion, , V is the volume, the initial volume.

We shall use the following laws:

 

·            Law of linear expansion:  

·            Law of surface expansion:

·            Law of volume expansion:

In our computation, we consider that: .

The surface of the torus can be calculated by the following formula

We will now show the formulas for the expansion forces and how we obtained them. First, the Hooke’s law on linear elastic springs:

 ,   is the elongation

,   is the elastic coefficient

We know the formula , where S is the section area and E the modulus of elasticity. We take into account that .

The expansion force has the following formula:

. From the formulas we obtain:

.

We know that to produce pseudogravity we have to induce a rotation movement to the torus. The value of rpms must be similar to Earth’s. Therefore, we have to induce a rotation movement of about rpm. The torus will move permanently, rotating with the determined speed. The torus will be exposed to the Sun’s rays and will expand in time. Because the torus is rotating permanently, different sections of the torus will be exposed to the Sun’s rays and will expand in time. We also have to take in consideration that the unexposed parts will contract. Contraction also varies with time. We can assume that the expansion and the contraction and the expansion forces depend on the time. We determine that , because different parts will be exposed in different moments of time, and so will those parts expand.

We will now write the expansion equations:

 

 

 

Because the rotation speed is constant,  will vary periodically and its graph will be almost a sinusoid.

If we consider our torus as an isotropic body, we can consider the following formulas for determining  and  in proportion with .  Remark: We consider the torus isotropic, so that the material has the same properties in all the directions. Otherwise, the following formulas are not correct. We deduce the following formulas in the calculus:

 

 

We consider negligible. Therefore: ,

These formulas can prove important in the calculus of the volume expansion. The volume expansion will be:

 

 

The initial volume will be calculated as follows:

.

 

But, because only 50% will be exposed, the initial volume will be:

 

By changing in the formula we obtain:

 

We will calculate the expansion of the surface by the following formula:

 

, where r is the minor torus radius.

 

Remark: We consider the torus is not empty, with the same material  constant all over the torus. The force of expansion will be:

 

 

If we consider that the torus is not filed in with the same material, we must analyze the torus in sections. We compute the volume of each section. By knowing that the sections are made of different materials, the system will act different.

We remark that the forces of expansion will tend to expand the half illuminated part of the torus, while the contraction forces (equal in modulus) will contract the dark side of the torus. This will lead to a “scissoring” effect: the system will be torn apart. We can see the effect of the forces upon the torus in figure VII.3.

This effect is dangerous, because it can destroy the torus by the great differences in mechanical expansions between the two halves. This effect must be damped; therefore we designed a “spring-like” system that may leave the torus halves place to expand/contract, without being affected by the scissoring effect. The system is presented in figure VII.4.

The vibrations induced by the expansion of one side, while the other contracts are analyzed in this chapter. We designed a system to prevent the torus’s destruction due to the scissoring effect.

The system is a solution to the problem. We can eliminate the rigidity of the torus if we separate the torus into several modules and unite them through a “tampon sphere”. The tampon sphere is a sphere of steel that will offer the system the elasticity needed to expand and contract without harmful consequences to the system. The spheres offer good elasticity and inside the spheres are the separation points between the modules. The modules are separated; therefore one part can expand while the other module contracts without being harmful to the system. Because this solution is the only one reliable in space, the shape of the space settlement will not be a perfect torus.  This solution is schematically presented in figure VII.4.

We now continue the calculus and we use a particular case: :

 

 

Due to the periodical rotation and exposure to the Sun, the system oscillates. The oscillations are considered stationary oscillations. Therefore, we can determine the frequency and wavelength of these oscillations to determine if they can affect the oscillatory system. We will use the following formulas to determine the wavelength and frequency of the oscillations:

 

 

But, we know that:

 

 

 

Therefore, the period T is:

,   where we consider that .

 

We obtain that:

 

In the formulas, we have used the following notations:

 

the number of semi wavelengths in the torus;

the wavelength;

the length of the torus;

the period for the stationary oscillation with the corresponding number of wavelengths;

the wave’s speed.

 

We considered all these formulas for the stationary waves that form in the torus due to the contraction and expansion of its modules. The contraction and expansion of the modules, varying in time, will induce oscillations in the torus’s body, even though the “scissoring” effect has been solved. Figure VII.5 shows a case of stationary oscillations.

It is known that for some wavelengths and frequencies chaotic vibrations may appear. Chaotic vibrations can destroy the oscillatory system and must be damped. We will discuss in the Chapter VIII about chaotic vibrations.

 

 

 

 

 

Figure VII.1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Figure VII. 2

Figure VII.3 shows how the part of the torus exposed to the Suns rays expands, while the unexposed part contracts. Also the temperatures are shown in Kelvin degrees. The sections of the torus are shown and a thermal isolating layer is shown in the structure of the torus.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Figure VII.3

 

Figure VII.3 shows how the expansion and contraction forces may influence the torus. The torus can be torn apart by the great differences between the contracted part and the expanded half.

 Figure VII. 4

Figure VII.4 shows how we separated the torus into modules separated by “tampon spheres”. This term is explained in the chapter VI. The figure illustrates the separation between modules inside the tampon sphere.

 

Figure VII.5

 

 

CHAPTER VIII

 

Vibrations and Chaos

 

By Horia-Mihail Teodorescu

 

In this chapter I am going to explain chaotic movements and vibrations and how to avoid them. I consider the torus to be like a huge spring, because its body is elastic. Indeed, we can see the torus as an elastic spring because it is made of metals – which are very elastic materials.

Chaotic vibrations can be induced in the torus structure by the couple of forces that make the torus move. Any metal has its elastic non-linearity. A non-linear spring may support chaotic vibrations.

On one side, the centripetal force tends to enlarge the spring; other forces, like those produced by heating and cooling, make the spring compress or expand. This may induce a chaotic vibration in the system.

If we see the torus as a huge elastic spring, we will see that a very important problem, yet not solved, is what happens if chaotic vibrations appear? The non-linearity of this spring (determined by the material used mostly in the construction of the torus), may determine that chaotic vibrations occur.

This problem of determining and damping the chaotic vibration has never been solved and is a major problem in our design. Chaotic vibrations may determine that the whole structure collapses.

Remark: When in movement equations nonlinear terms appear like the space at square/cube etc., acceleration, and speed at square/cube etc. the movement (dynamics) of that object is called non linear.

 

Definition: In the case of nonlinear dynamics there can appear the so-called chaotic movements that are not periodical, either uniform (uniform accelerated of with constant speed). It has been demonstrated that the chaotic movements or vibrations do not appear in the case of linear dynamics.

We will analyze an elementary case. We will consider an approximation, considering that the torus’s mass is concentrated in two symmetrical parts of the circle (see Figure VIII.1). The two masses are equal to half the torus’s mass. In equilibrium, the two masses are on the circle’s horizontal axis.

In my model, the two parts are connected by elastic springs on both sides to form the torus’s circle. The springs are identical and have equal coefficients. (See figure VIII.2) When the torus is illuminated by the Sun, the illuminated part will expand, while the unexposed part will compress. The inertia of the two masses will play a part in the overall movement, involving inertial forces, dilatation forces and elastic forces.

The total length of the springs plus the length of the masses is constant (it is equal to  = the torus’s length). When the exposed to the Sun’s ray’s spring is heated and expands with , the unexposed to the Sun’s rays spring cools and compress’s its length with . When “released”, the “springs” will produce oscillations.

We will consider the following elastic spring force, which is not linear:

 

 

Therefore, x²(t) is a square term and we have two elastic coefficients:  and .

We used the following notations:

·         is the mass coordinate, which varieties with time.

·         And  are the spring’s coefficients.

We will have the following movement equation:

We noticed that nonlinear dynamics may occur.

We analyzed a very much-simplified case. In a better approximation we consider the torus as a multitude of masses tied by identical smaller springs. Each spring will have the same coefficient and the masses will be equal. When n, the number of masses will increase, then each mass’s weight decrease. Then, the approximation will be more refined.

In the simplified case we know that we may obtained chaotic vibrations. When the torus will rotate, the elastic spring force will vary with time (), because the heating by the Suns rays and cooling is produced at different positions on the torus. In this hypothesis, we don’t know if chaotic vibrations will still appear, because they might be damped. But, it is possible that chaotic vibrations will occur without being damped.

The movement equation we have determined is a nonlinear equation. The only way to determine its solutions is by calculus. A computer makes the calculus.

Because computers are discrete machines, we have to discretize the derivatives for the machine to calculate it.

Approximating derivatives for the numeric calculus in the calculating program of the functions  is called discretizing.

 

 

Definition: The process of approximating a limit is called discretizing.

 

In our case, to calculate the limit, we must approximate it, so that . For  we will use the following formula:

 

 

and for  the following formula:

 

 

We also made a program in Borland C for DOS that analyses the chaotic movements for equations of motions with simple nonlinear terms. The program shows three diagrams:

1.      Diagram of space in compared to with time:  space in compared to with the time t.

2.      Phase diagram: diagram of space in compared to with the speed in the time t.

3.      Bifurcation diagram: a diagram that affords the user to determine chaotic movements in a graph of space in compared to with a coefficient of the space.

I have obtained chaotic oscillations with my program for several non-linearities.

 

Fig. VIII.1. Shows an approximation with two masses and 2 springs

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Figure VIII.2

 

 

 

 

 

 

 

 

 

Chapter IX

 

Locating the space settlement

 

By Horia-Mihail Teodorescu

 

 

In this chapter we are going to discuss about how to locate the space settlement in space. In this chapter we are treating important problems, like how to locate the station in stable orbit and how this orbit should be. We treated also about the LaGrange libration points and located the station using the LaGrange libration points. Much of the computations are done by myself, with some corrections by the teachers, but I have not copied them from books.

First, if we locate the station in a geo synchronous orbit, we will obtain the following equations (see figure IX.1):

 

·            The centrifugal force is:

 

,

where:

m is the mass of the body,

 Is the speed of the body,

     Is the ray (in our case the distance between Earth as a point, the center of the orbit, and the station).

 

·            The attraction force upon the station will be:

, the law of universal attraction.

In the formula we will have:

Is the constant of universal attraction,

The mass of the first body (in our case the Earth),

The mass of the second body (in our case the station),

Is the distance between the two bodies.

 

Notice: We consider the two bodies as points in respect to the distance between them.

We will obtain a dynamic equilibrium for:

 

 

We also know that: . Therefore:

 

 

 

The case of 3 bodies at rest

 

We will consider that we have included in our calculus the Sun and the Earth and the station as a point on the line Earth-Sun. Figure III.2 shows the forces upon the station and how we arranged the station. This is a simplified calculus, which has no real physical sense, as the bodies can not remain in fixed positions, due to attraction.

We will consider the station in the point L on the line Earth-Sun.

We consider the point L a point of equilibrium. If the Earth is immobile, we will have the following equations:

We consider that we know and . We have made the following notations:

 Is the mass of the Earth;

 Is the mass of the Sun;

 Is the mass of the space station;

Is the distance between the Sun and the station;

 Is the distance between the Earth and the station;

Is the constant of universal attraction.

 

We also know the distance between the Earth and the Sun, distance D. Therefore, we will derive that:

 

 

By considering the last obtained formula in the main equation we will obtain:

 

From the last formula we will obtain that:

 

 

By determining , we will obtain the points of equilibrium L.

 

 

Third case

 

In this case we will analyze how the station moves yet remaining on the axis Earth-Sun and is rotating at the same time with the Earth around the Sun.

For this case we will consider the figure IX.3.

By analyzing figure IX.3 we obtain that upon the station the following forces act: , , . We know that:

 

We consider as the force of attraction between the Sun and the station and as the force of attraction between the Earth and the station.

We will consider in figure IX.3 as the point  a point of equilibrium in which the station is shown.

We will show the conditions for equilibrium in the point :

 

where:

We also know that:

Therefore, by changing v in the equation, we will obtain:

 

 

From this fifth degree formula in we understand that we will have maximum 5 L points for which the values will satisfy the equation.

The equation can have 5 real number solutions possible, therefore two will probably imaginary number solutions on the Earth- Moon axis.

The three-L points found will be the libration points , , . Therefore, we have found three possible orbital points as solutions. We will find next the other two-libration points and will determine the orbit solution for out station.

 

            Other equilibrium points

 

            We know that there are 2 more equilibrium points, named Lagrange L4 and L5. These points are considered by many the best positions for the space settlement.

 

 

 

Figure

 

Figure IX.1 shows an orbiting object (satellite, space station) in a geo synchronous orbit and shows the forces that act on the orbiting object.

 

 

Figure IX.2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Figure IX.2 shows what forces act upon the orbiting object (satellite, space station) and how we obtained the Lagrangian libration points ,  and .

 

Figure IX.3

 

Figure IX. 3 presents the forces which act upon the orbiting object (space station, satellite) when the orbiting object is rotating around the Sun with the same angular speed as the Earth.

 

 

ANNEX

 

By Horia-Mihail Teodorescu

Phase diagrams

 

Definition: A phase diagram of a movement means representing the movement in the coordinates plan space (on the Ox axis) – speed (on the Oy axis).

 

Remark: The representation is made point-to-point for successive moments of the time t.

 

In the phase diagram we have the following cases:

 

·           The object does not move => x(t) constant, v(t) constant; the trajectory is reduced to a point in the horizontal axis;

·           Periodical harmonic movement (sinusoidal) => x(t)=sin(t), v(t)=cos(t) => x²+y²=1. The graph is a circle with the centre in O;

·           Whatever kind of periodical movement is represented by a closed curve (at which the end and the beginning are the same);

·            A chaotic movement is given by a closed curve that fills an area of the plan. The figure obtained so is called strange attractor.

 

The equation of a circle in a plan is given by:

 

 Is the equation of a circle with the centre in the points of coordinate (a, b) and ray R.

 

 A few informatics elements

 

Drawing a line when we know the end points of the line (in ANSI C):

            line(x-start, y-start, x-end, y-end);

The color must be set before by setcolor(the color preferred);

 

For the phase diagram there has to be given the following elements:

 

·           x-start= x(t-1);

·           y-start= v(t-1);

·           x-end= x(t);

·           y-end= v(t).

 

We represent v(t) as being:

v(t)=x(t)-x(t-1)

v(t-1)=x(t-1)-x(t-2)

 

After definition, for a phase diagram we need the coordinates space- on the horizontal axis (Ox and the coordinates speed- on the vertical axis (Oy to draw a point-to-point graph for the different values of t after which x(t) changes that we can compute in the program in a for loop and after the speed’s values we obtained it after the formula:

.

 

Bifurcation diagrams

 

Definition: The bifurcation diagram is the graph of all the given values of x(t) from the differential equations (the physical interpretation we find compared to the situations:  etc.) compared to a coefficient of the equation.

 

Remark: For many coefficients of the equation we obtain different bifurcation diagrams.

 

Equation examples I used in my programs:

 

 Where a is the coefficient.

 

There are a few general models of formulas analysed by the program:

 

1.        ;

2.        ;

3.        ;

 

 

 

References for TEBA.1

 

NASA: Space Settlement Design Competition GLOSSARY. http://space.bsdi.com/p.glossary.html

 

The NASA-Ames/Stanford 1975 Summer Study. Space Settlements: A Design Study. http://lifesci3.arc.nasa.gov/SpaceSettlement/75SummerStudy/Table_of_Contents1.html

 

Al Globus: Space Settlement Basics, ttp://lifesci3.arc.nasa.gov/SpaceSettlement/Basics/wwwwh.html#how-much

 

David R. Criswell: The Initial Lunar Supply Base. NASA Sp-428. Space Resources And Space Settlements. V-1. http://Lifesci3.Arc.Nasa.Gov/Spacesettlement/Spaceres/V-1.Html

 

Jack Spurlock, William Cooper, Paul Deal, Annita Harlan, Marcus Karel, Michael Modell, Paul Moe, John Phillips, David Putman, Philip Quattrone, C.David Raper Jr., Elliot Swan, Freida Taub, Judith Thomas, Christine Wilson And Ben Zeitman: I-2. Research Planning Criteria for Regenerative Life-Support Systems Applicable to Space Habitats. NASA Sp-428. Space Resources And Space Settlements. I-2. http://lifesci3.arc.nasa.gov/SpaceSettlement/spaceres/I-2.html

 

William H. Arnold, Stuart Bowen, Kevin Fine, David Kaplan, Margaret Kolm, Henry Kolm, Jonathan Newman, Gerard K. O'Neill and William R. Snow: Mass Drivers III: Engineering. NASA SP-428. SPACE RESOURCES and SPACE SETTLEMENTS. III-3. http://lifesci3.arc.nasa.gov/SpaceSettlement/spaceres/III-3.html

 

STUART M.LEE: Lunar Building Materials - Some Considerations on the Use of Inorganic Polymers. V-3. NASA SP-428. SPACE RESOURCES and SPACE SETTLEMENTS. V-3. http://lifesci3.arc.nasa.gov/SpaceSettlement/spaceres/V-3.html

 

D. Bhogeswara Rao, U.V. Choudry, T.E. Erstfeld, R. J. Williams and Y.A. Chang: Extraction Processes for the Production of Aluminum, Titanium, Iron, Magnesium and Oxygen from Nonterrestrial Sources # V-5. NASA SP-428. SPACE RESOURCES and SPACE V-5. SETTLEMENTS. http://lifesci3.arc.nasa.gov/SpaceSettlement/spaceres/V-5.html

 

Richard J. Williams, David S. McKay, David Giles and Theodore E. Bunch : # V-6 Mining and Beneficiation of Lunar Ores. . NASA SP-428. SPACE RESOURCES and SPACE V-5. SETTLEMENTS. V-6. http://lifesci3.arc.nasa.gov/SpaceSettlement/spaceres/V-6.html

 

NASA 0- JPL: Basics of Space Flight (Basics of Space Flight Learners' Workbook). Chapter 7. Mission Inception Overview. http://www.jpl.nasa.gov/basics/bsf7-1.html

 

NASA 0- JPL: Basics of Space Flight (Basics of Space Flight Learners' Workbook). Chapter 11. Typical Onboard Systems. http://www.jpl.nasa.gov/basics/bsf11-4.html

 

SOLAR SAILS. http://www.u3p.net/admin/qqm_a.htm. Union pour la Promotion de la Propulsion Photonique. Webmaster : [email protected] Updated October 2001. © U3P / Olivier Boisard - 1994-2001

 

Mark Cummins, Lorraine Murphy, Stuart Redmond, Alison Squire, Cian Wilson: DAEDALUS. A Space Settlement Design. (2000) http://www.daedalusal4.utvinternet.co.uk/cover.htm

 

The Babylon Project: - On The Edge of a New Frontier. A Space Settlement Design Study by: Thomas Beatty and David Peters. Advised by Victor Mazmanian of Greenwich High School. Winner of The 1998

 

Centurion Space Settlement -Our Gateway To Space. A Space Settlement Design Proposal by Azhar Syed Azmi. Vienna International School, Grade 10. 2001 Grand Prize Winner of the NASA Ames Space Settlement Design Contest http://lifesci3.arc.nasa.gov/SpaceSettlement/Contest/Results/98/winner/

 

Boeing Satellite Systems. http://www.boeing.com/defense-space/space/bss/flash.html

The Boeing Company. XIPS: The Latest Thrust in Propulsion Technology, http://www.boeing.com/defense-space/space/bss/factsheets/xips/xips.html

 

Eugene Butikov, Three-body motions in the equilateral configuration. Eugene Butikov personal page. http://www.ifmo.ru/butikov/Projects/Collection6.html#_applet

 

David P. Stern: From Stargazers to Starships (home page of a book-on-the-web: http://pwg.gsfc.nasa.gov/stargaze/Sintro.htm)

 

NASA Computer for Essential Figures - Computer assisted design (CAD). http://lifesci3.arc.nasa.gov/SpaceSettlement/designer/sphere.html

 

Dr. David H. Hathaway, (Mail Code SD50, NASA/Marshall Space Flight Center, Huntsville, AL 35812): The Solar Wind. http://science.nasa.gov/ssl/pad/solar/sun_wind.htm

 

Dr. David H. Hathaway, ([email protected], (256) 961-7610. Mail Code SD50, NASA/Marshall Space Flight Center, Huntsville, AL 35812) The Solar Dynamo. http://science.nasa.gov/ssl/pad/solar/dynamo.htm

 

Designing a Space Station. Lesson Title: Designing a Space Station. http://www.sciencenetlinks.com/lessons.cfm?BenchmarkID=3&DocID=141. Also, http://www.sciencenetlinks.com/pdfs/design_actsheet.pdf. Copyright AAAS 2002.

 

International High School Space Settlement Design Competition. http://space.bsdi.com/p.train.html. Also “Training material”, http://space.bsdi.com/p.train.html, including Solar Power in Space. http://space.bsdi.com/p.solar.html

 

T.A. Heppenheimer: L5: A Place in Space. http://www.l5news.org/L5whatis.htm [[It turns out (from an extremely messy calculation done only in 1968) that with the Sun in the picture, a colony could be placed not directly at L4 or L5, but rather in an orbit around one of these points. The orbit keeps the colony about 90,000 miles from its central libration point.]]