"The Earth is the cradle of Humanity. But one doesn�t always live in the cradle. " Konstantin Tsiokolvsky
Once decided that the settlement will be established in outer space itself and not in any planetary or lunar surface, the next step would be determining exactly where in space to place it.
Whatever point or trajectory is chosen, it must be consistent with the before mentioned objective of colonizing space. Therefore, the colony has to be placed in a stable and predictable orbit or trajectory that can allow for the human and scientific objectives of the Mission to be met.
The other alternative, that will be evaluated later in the text, would be placing the colony in an outbound trajectory from the Solar System to try to explore interstellar space and possibly to reach another star.
Although the relative advantages and disadvantages of each of the options that are open will be thoroughly evaluated before reaching a final decision, at a first glance it seems desirable to place the settlement, at least in its initial stages of development, as near to the Earth as possible, that is, in Near Earth Space or within the Earth-Moon system. This is so for the following reasons :
Trips are shorter: In any circumstance, it will be advantageous to have a short transit time between the settlement and the Earth. This becomes obvious in cases of emergencies where assistance or supplies would be needed from Earth.
Availability of materials : Materials and supplies will be needed for both the building and development of the colony. The Earth and the Moon will be sources of building materials and supplies and being near them will speed the process and make it more economical.
Time lag: Although radio waves travel at the speed of light, the immense planetary distances cause a delay in voice communications, telemetry and remote operation of devices. This becomes noticeable within the range of, for example, the distance between the Earth and Mars, not allowing, for example, real time remote control or monitoring. Within the Earth-Moon system the time lag in communicatons is hardly significant.
If we let an object free in the air, we will immediately notice that it will fall towards the Earth. In fact, all bodies, when left free, will be attracted towards the Earth.
We know already that, for an object to change its speed, that is, to be accelerated, a force must be supplied. The Earth exerts a force over every object, and that is why they fall towards it. That force is the weight of the object. Every one of us is familiar with his own weight.
The weight can be defined then as the force with which the Earth attracts any given object.
If we let two similar objects fall from a certain height, we can see that both of them will hit the ground with identical speed. This is because the acceleration with which all objects fall is the same. This acceleration is called gravity.
We can then formulate the equation, following Newton's first law :
F = m . a
In this case, the force is the weight and the acceleration is the gravity. The equation will then read :
W = m . g
Isaac Newton also discovered that any two objects attract each other with a certain force. However, this force is not significant unless the mass of the objects is very big. The formula that expresses the relationship is :
F = G . m1 . m2 / d ^2
Where G is a constant, m1 and m2 the mass of the objects. d is the distance that separates them. We see then that if the masses of the objects are big, the force will increase, and if they are at a short distance the force will increase again.
As we have said, this force is barely perceptible in normal cases. If this was not so, we would be hauled into other persons or buildings. However, when one or two of the objects possess an enormous mass, as in the case of the Earth, the force is important.
If we substitute in the formula our mass and the mass of the Earth respectively, and then the distance to the center of the Earth, we will find that the force found will correspond exactly to our weight.
This same formula explains why our weight is reduced when we ascend. As the distance to the center of the Earth is increased, the force decreases. Nevertheless, this decrease is hardly noticeable because the magnitude of the ascent is insignificant as compared to the radius of the Earth.
A person will weigh less in the Moon due to lower gravity. The force with which it pulls a person is 6 times less than in the Earth. The weight in any given planet depends on the gravity. However, the mass of an object is invariable. The mass measures the "quantity of matter" or substance in an object and that will obviously not change in another planet's environment.
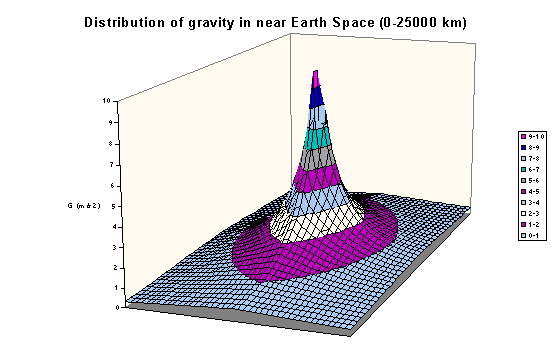
Distribution of Gravity in Near Earth Space
In order to start thinking of regions in space in terms of their
gravity, it is a good idea to map the distribution of gravity on
Near Earth Space. 
If the values are substituted in the formula for gravitation at a point x,y (taking the Earth as the origin of the coordinate system) then the value of gravity at any point x,y can e found by :
g(x,y)= G MEarth / (x^2+y^2)
where G = 6.67 x 10^ -11 N m2 / kg
and MEarth = 5.98 x 10^24 kg
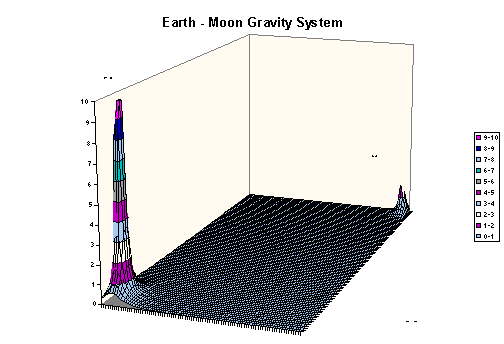
Another interesting visualization is that of the gravity distribution in the Earth-Moon system. The gravity of the Moon at a point x,y (again using the Earth as origin and placing the Moon on the x-axis) would be :
g(x,y)= G MMoon / [(R-x)^2+y^2]
where R (mean distance from the Earth to the Moon)= 3.85 x 10^8m
and MMoon = 7.36 x 10^22 kg
Newton's second law, the principle of inertia states that an object tends to remain in the state of rest or uniform speed. This is known as the inertia of the body.
We can experience the effects of inertia when we are traveling forward and we brake or try to stop. Our body, due to inertia, tends to continue going forward. In the same way, when we accelerate, we tend to "sink" in our seats, again due to inertia.
The same happens, but now with more dramatic effects, when we take a curve. The object tends to continue in its straight course, and when we start turning we feel a force that pulls us away from the center of the curve. This is an inertial force, called the centrifugal force, which always points in a direction opposite to the center of the curve.
We can feel this force when riding a bicycle. We are forced to tilt the bicycle in order not to be overturned by the centrifugal force.
The magnitude of this centrifugal force is related to the mass of the object, its speed and the radius of the curve. The expression is the following :
Fc= m . V^2 / R
where Fc : the centrifugal force
m : the mass of the object
V : the speed of the object
R : the radius of the curve  An object in a circular orbit around the Earth.
An object in a circular orbit around the Earth.
Analyzing the formula, several conclusions can be formulated. The higher the speed, the bigger the centrifugal force will be. We know from our own experience, from driving a car or riding a bicycle, that in order to negotiate a curve successfully the speed must be reduced.
We can also see that if the radius is small, the force will increase. A curve with a small radius is what we call a sharp turn, while a curve with a large radius is a smooth one. The sharper the turn, the greater the force will be.
When spacecraft go into outer space, they frequently circumnavigate the Earth in what are called orbits. An orbit is a circular or an elliptical path around the Earth.
In an orbit, two basic forces act over the object : its weight, pulling it down towards the center of the Earth, and the centrifugal force, pointing away from the center of the orbit, in this case, the center of the Earth. If the weight is bigger than the centrifugal force, the object will fall back into the Earth and so reduce the radius of its orbit. If the centrifugal force is greater than the weight, the craft will tend to escape from the Earth and so the radius of its orbit will grow. If the weight is equal to the centrifugal force, the object will remain in equilibrium and, as there is no friction in space, maintain its orbit endlessly.
If we consider any given body of mass m and the Earth, the formula for the attractive force would be :
W= G.m.Me/R^2
W is the weight (the weight is obviously the force with which the Earth attracts any body or object) and R the radius of the Earth, supposing that all the Earth's mass is concentrated at its center.
According to Newton's first law :
F= m.a
The acceleration can be determined by dividing force by mass:
a= F/m
In the case of weight, the acceleration would correspond to gravity :
g= W/m
For an orbit to remain stationary, the centrifugal force must equal the gravitational attraction of the Earth (weight) :
Fc= m.V^2/(R+r)
where R is the radius of the Earth and r the radius of the orbit above Earth's surface (see figure)
Weight was :
W= G.m.Me/(R+r)^2
(a person's weight would descend in a higher orbit, because g will decrease with height)
Equaling the centrifugal force with weight :
m.V^2/(R+r) = G.m.Me/(R+r)^2
Finding out V :
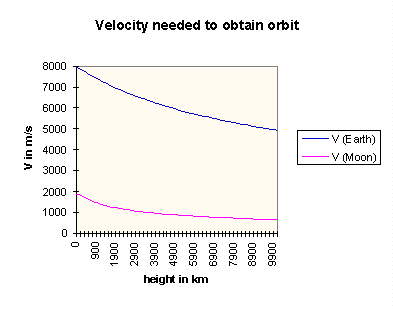
V= [G . Me / (R+r)]^1/2
which is finally the expression for the velocity V needed to obtain an orbit of radius r
The following graph shows the relationship between the height of
the desired orbit and the velocity needed : 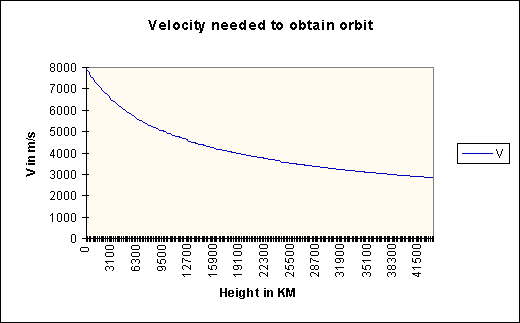
| ADVANTAGES | DISADVANTAGES |
| Communications: Because of its proximity with Earth, and the fact that several revolutions are made per day, communications are both easy and fast. The time lag is negligible, which allows for remote operation from ground. | Short days and nights : In LEO, the Space Colony would have a far greater angular speed than the Earth. This means that it would encounter several dawns and sunsets per day, which would not allow an efficient utilization of solar energy |
| Earth observations. For the same reasons as above, the Earth can be explored and studied from space. Much is yet to be learned about our Blue Planet, and having a space colony directly orbiting the Earth would boost Earth observations tremendously. | Limited access to solar energy. For the same reason mentioned above, the availability of solar energy would be very much limited. |
| Rapid transit : Perhaps the greatest advantage of a LEO space colony stems from the fact that a trip to and from it would only take a few hours, allowing for eventual rescue missions, servicing, resupplying. etc. | Debris in orbit. LEO is scattered with debris from spacecraft, satellites, space stations, etc. This is a potential danger to the less rugged parts of the colony. |
| Station keeping problems : All orbiting spacecraft require a minimum of thrust to compensate for slight deviations in orbital path due to space environment interactions, solar wind etc. Maintaining a stable orbit would require enormous precision and considerable energy. | |
| A relatively dangerous place : If for some reason, like in the case of Skylab, its orbit were to decay and the colony fall back into Earth its massive size would make it potentially very dangerous. | |
| Energy to get in orbit : Most of a rocket�s thrust is consumed to overcome the earth�s gravity well (see Near Earth Gravity diagram) So in terms of energy and thrust it doesn�t really make too much difference whether the space colony is in LEO or in the rest of the Earth-Moon system. | |
| Distance to the Moon and asteroids : If materials are to be extracted from the Moon and asteroids, a location in LEO would hardly be advantageous. |
Geosynchronous orbits are those in which the orbiting spacecraft or sattellite rotates around the Earth with the same angular velocity as the Earth. This means that the object will remain in constant longitude with respect to Earth. If the orbit has a certain inclination, the apparent movement of the object would be along a certain meridian. In the specific case of an equatorial orbit (0° inclination), there would be no apparent movement along the meridian. Thus, the object would be fixed or stationary on top of a certain spot along the Equator. These special types of geosynchronous orbits are called geostationary orbits .
The Earth's angular speed is determined by the fact that it rotates 360° (2 p) in approximately 24 hours.
w = 2 p / (24x3600s) = 7.3 x 10^-4 /s
There is only one radius or height for a geosynchronous orbit. At such, the velocity needed to obtain orbit must result in an angular velocity equal to that of the Earth . The centrifugal force expressed in terms of the angular velocity is :
Fc= m.w^2.(R+r) To find out the radius r of a geosynchronous orbit we must again equal the centrifugal force to the weight or gravitational attraction :
m.w^2.(R+r) = G.m.Me/(R+r)^2 Finding out r :
r = (G x Me / w^2 )^1/3 = 3.587 x 10^7 m That is, a geostationary orbit would take place at approximately 36.000 km.
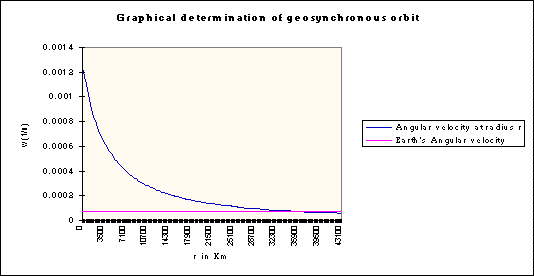
These orbits could still be considered Low Earth Orbits (1/10th of the Earth-Moon distance) so their advantages and disadvantages replicate those previously outlined for LEO. Unique advantages for geosynchronous orbits are the following:
- Fixed point over Earth : Being over a fixed point or at least spanning the same longitude enables easy contact, which would result in uninterrupted communications and full time monitoring. - Earth study : Although the area encompassed will be limited, permanence over that area or point would enable in depth scientific study of the Earth.
Any body in outer space would be subjected to various gravitational forces. In theory, every one of the celestial bodies would exert a certain gravitational attraction on the spacecraft. However, it is only practical to consider the gravitational fields of those planets or bodies that are relatively near to the point considered. Several points in space have to exist in which the main gravitational forces balance, allowing an object in its vicinity to remain stable in a state of neutral buoyancy. The determination of such points considering the nine planets and the Sun is extremely Because of the gravity valley existent in the libration points (also known as Lagrangian points) bodies tend to drift towards them and remain there. In the Solar System the so called Trojan asteroids can be found in the Libration points. This same reason makes the possibility of situating the settlement in a libration point an attractive one to consider. Because of proximity, the first obvious choice would be the Earth-Moon libration points.
 Libration points
along the Earth Moon system
Libration points
along the Earth Moon system
For the following analysis we will just consider the gravitational attraction of the Earth and the Moon. Although a third influence, that of the Sun, would be noticeable, its consideration would make the problem too complicated to resolve and the values of the forces are practically negligible in the determination of the position. Whatever object stays relatively fixed with respect to the Earth-Moon system must in that way rotate along with the system, with the same angular speed that the Moon rotates with respect to the Earth. Because of this rotation the inertial force that pulls the object away from its center of rotation (what we have called centrifugal force) must also be considered. An immediate analysis of the gravitational and inertial forces shows that at least three libration points must exist along the Earth-Moon system : one of them between the Earth and the Moon, another one behind the Moon and finally another one behind the Earth.
At a certain point distant x from the Earth, the gravitational attraction of the Earth will be balanced by the gravitational attraction from the Moon and the inertial centrifugal force.
Fe = Fm + Fc Fe (gravitational attraction of the Earth) :
Fe = G Me . m / x^2 Fm (gravitational attraction of the Moon) :
Fe = G Mm . m / (d-x)^2 Fc (centrifugal force) :
Fc = m.w^2 .x where w is the angular speed of the Earth-Moon system
The Moon makes a complete revolution around the Earth in 27 days, 7 hours and 43 minutes. This means that :
w = 2 p / (27 x 24 x 3600 + 7 x 3600 + 43 x 60 ) 1/s = 2.66 x 10^-6 Replacing in the equation,
G Me . m / x^2 = G Mm . m / (d-x)^2 + m w^2 x Fm (gravitational attraction of the Moon) :
Fe = G Mm . m / (d-x)^2 Fc (centrifugal force) :
Fc = m.w^2 .x where w is the angular speed of the Earth-Moon system The Moon makes a complete revolution around the Earth in 27 days, 7 hours and 43 minutes. This means that : w= 2 p / (27 x 24 x 3600 + 7 x 3600 + 43 x 60) 1/s = 2.66 x 10^-6 1/s Replacing in the equation,
G Me . m / x^2 = G Mm . m / (d-x)^2 + m w^2 x x then results to be approximately :
x = 320000 km 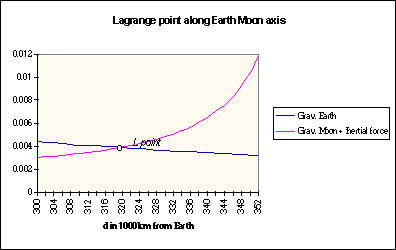
At a certain point behind the Moon, the gravitational force of attraction of the Earth and the Moon add up and will have to be compensated by the inertial force of rotation (centrifugal force) to find a libration point. If the point is at a distance x behind the Moon :
Fe + Fm = Fc G Me . m / (x+d)^2 + G Mm . m / x^2 = m w^2 (d+x) where x is approximately 67000 km.
Another libration point could exist behind the Earth, along the Earth-Moon axis. At this point, the gravitational attraction of the Earth is added to that of the Moon and has to be compensated by the inertial force. If the point is at a distance x from the Earth :
Fe + Fm = Fc G Me . m / x^2 + G Mm . m / (x+d)^2 = m w^2 x Finding out x, it results to be :
x = 326000 km
At a certain point behind the Moon, the gravitational force of attraction of the Earth and the Moon add up and will have to be compensated by the inertial force of rotation (centrifugal force) to find a libration point. If the point is at a distance x behind the Moon :
Fe + Fm = Fc G Me . m / (x+d)^2 + G Mm . m / x^2 = m w^2 (d+x) where x is approximately 64000 km.
Another libration point could exist behind the Earth, along the Earth-Moon axis. At this point, the gravitational attraction of the Earth is added to that of the Moon and has to be compensated by the inertial force. If the point is at a distance x from the Earth : Fe + Fm = Fc G Me . m / x^2 + G Mm . m / (x+d)^2 = m w^2 x Finding out x, it results to be :
x=383000 km approximately.
Other libration points exist in the Earth-Moon system that are
not situated along the Earth-Moon axis. If we generalize the
analysis, the same forces have to be balanced in their projections
along the x and y axis
. 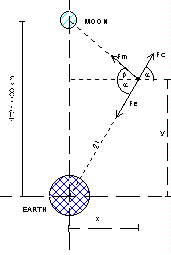
At a point x,y :
d1=[(d-y)^2+x^2]^1/2
sin a = y/(x^2+y^2)^1/2
cos a =x/(x^2+y^2)^1/2
sin b = (d-y)/[x^2+(d-y)^2]^1/2
cos b = x/[x^2+(d-y)^2]^1/2
Fc = m.w^2 (x^2+y^2)^1/2 (centrifugal force)
Fe = m Me.G/(x^2+y^2) (Gravitational attraction of the Earth)
Fm = m Mm.G/[x^2+(d-y)^2] (Gravitational attraction of the
Moon)
Along the y axis :
Mm .G (d-y)/ [x^2+(d-y)^2]^1/2 + w^2 y - Me .G.y/(x^2+y^2)^3/2 =0
Along the x axis :
- Mm .G x/[x^2+(d-y)^2]^3/2 + w^2 x - Me .G.x/(x^2+y^2)^3/2 =0
The solution of this equation yields two points along the Moon�s orbit, both at 60° from the Earth- Moon axis.
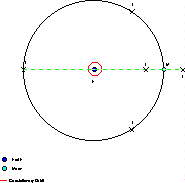 The Lagrangian
Points
The Lagrangian
Points
In the precedent analysis, for simplicity reasons, we have just considered the gravitational forces of the Earth and the Moon, thus neglecting the important influence of the major celestial body in the Solar System, the Sun. If the gravitational attraction of the Sun is considered, none of these Lagrangian points are really stable. In order to maintain stability, a eventual space colony would have to be placed in an small elliptical orbit around the points.
In theory, any object in the libration points moving along with the Earth Moon system would remain (disregarding, as previously said, the influence of the Sun) indefinitely in neutral buoyancy.
However, if any disturbance were to move an eventual object away from those points, the outcome would be different for each of them.
As a first example, let�s analyze the first of the Lagrange points, situated some 326000 km away from the Earth between the Earth and the Moon. If an object is moved along the axis, for instance in the direction of the Moon, the forces will change in the following way :
Centrifugal force : if the angular velocity is to remain the same to keep pace with the Earth-Moon system, then the radius increases and so does the centrifugal force.
Moon�s gravitational attraction : If the object is placed closer to the Moon, obviously the gravitational attraction will increase.
Earth�s gravitational attraction : Inversely, if the object is displaced away from the Earth, the gravitational attraction of the Earth will be smaller.
So, if the object falls out of its equilibrium position, it will not return to the Libration points. This is a position of unstable equilibrium.
If the same analysis is repeated for the other two libration points along the Earth-Moon axis, the same phenomenon is observed. The three points along the axis are unstable, that is, if they are moved along the axis they will not return to their equilibrium positions. In a gravitational analogy, it could be said that they are similar to a plateau atop a hill.
The other two libration points, along the Moon�s orbit, are of stable equilibrium. If the object is moved away from the equilibrium position, it can be seen that the forces will tend to increase and decrease in such a way that the object will return to the libration point. These points can be assimilated to bowl shaped valleys.
Because of these considerations, any of the two libration points in the Moon orbit seems to be a better choice than the points along the axis and so will be considered in the ensuing advantages and disadvantages analysis.
| ADVANTAGES | DISADVANTAGES |
| Unlimited solar energy: Because the libration points are situated along the Moon�s orbit in a different plane from the earth�s orbit around the Sun, a space colony in any of those points will enjoy the ultimate benefit of permanent exposure to the Su | Debris : Because of its bowls shaped valley shape, the L points are a converging place for minor asteroids and other space debris. |
| Close to the Moon : The Moon is a plentiful source of construction and shielding materials. The Libration points are not too far off from the Moon, and eventually from the asteroids that could yield other elements not present in the Lunar surface. | Not really stable : It has been stated that the Sun�s influence determines a non perfectly stable L point, which means that some station keeping will have to be done. |
| Communications : The time lag for communications to an L point is approximately 1.3 sec, which constitutes an advantage over remote locations and enables remote operations (feedback in less than 3 sec.) | |
| Not too far from Earth : Although the L points are not too close to Earth, they are not so far away either. A transit time with Apollo technology would be in a few days. With advanced propulsion, travel to and from an L point would even be faster. How | |
| Easy station keeping : The gravitational stability of the libration points is advantageous as compared to other orbital paths in terms of automatic control of orbit by thrusters ion the case of instabilities originated in space environment interaction | |
| Lunar Outpost : The Lunar Outpost would be a necessary first step in the colonization of space and can be assumed to exist prior to the building of the Space Colony. The L points are relatively close to the Moon and this allows frequent interaction wi |
Another interesting possibility would be to place the settlement in Lunar Orbit. In the same way as the Earth�s gravity attracts a spacecraft and compensates that attraction with the inertial centrifugal force, the Moon�s weight could also be used to park the Colony in Lunar Orbit. The velocity needed to obtain a certain Lunar Orbit of height h can be found in the same way as it was done for the Earth :
Mm= 7.36x 10^22 kg (mass of the Moon)
Rm=1738 km (radius of the Moon)
G . m . Mm /(Rm+h)^2 = m. V^2 / (Rm+h)
Finding out V :
V = [G . m . Mm /(Rm+h)]^1/2
| ADVANTAGES | DISADVANTAGES |
| Close to the Moon : As it has already been mentioned, the Moon is a plentiful source for materials for construction and shielding. Being in Lunar Orbit ensures fast access to these supplies. | Limited solar exposure : A low lunar orbit will mean that half of the time the settlement will be hidden from the Sun�s rays by the Moon�s shadow. This obviously results in a limited access to Solar Energy. |
| Communications : Being within the Earth-Moon system still ensures a negligible time lag, quick and reliable communications and possible remote operation. | Station Keeping : Although velocities needed are smaller than in the case of LEO, they are still considerable and will require very careful monitoring. |
| Out from Earth : It�s quite close to the Earth in terms of communications but still far enough to try new propulsion systems and experiments, etc. |
A completely different idea would be not to place the Space Settlement in a fixed point or orbit in space, but rather to design a trajectory to take it along various points in the Solar System.
A presumably massive Space Colony could only have thrusters capable of performing minor corrections to its path. It is not a conceivable idea with today�s propulsion systems to think of a colony- spacecraft capable of traveling in space at will.
At most, what could be thought of are thrusters that could make necessary on course corrections to take advantages of gravity assisted trajectories and put the colony in orbit around planets or other celestial bodies. Once there, it could perform scientific investigations and then resume travel on to another objective.
The well known technique of gravity assist consists in utilizing a celestial body�s gravitational attraction to propel spacecraft further away from it in a desired direction. The planet or celestial body is also attracted and �gravitationally propelled� by the passing spacecraft but the effects are barely noticeable.
| ADVANTAGES | DISADVANTAGES |
| Multiple opportunities for investigation : Traveling from one point in space to another would give colonists very good chances of investigating the space environment and planetary objects. | Limited transmission of solar energy : If the space settlement is in transit around the Solar System, it is unlikely that it will receive permanently energy from the Sun, and even more unlikely that that energy will be able to be beamed back to Earth. |
| Propulsion : Although gravity assists would be used, some thrusters would be required for course corrections and orbit insertion and transfer. As the settlement is likely to become very massive, the calculation of these trajectories s bound to bec | |
| Communications : If the colony is to be settled in a planetary orbit, then depending on the chosen planet the time lag in communications could become unacceptably high, requiring absolute self sufficiency and not allowing remote operations. | |
| Varying conditions : Moving from one celestial body to another will considerably change the design constraints for the settlement. this means that in all aspects the colony would have to be prepared to make full use of space resources under totally di |
A very popular science fiction concept could be another possible alternative. The starship idea has been widely exploited in novels, movies and TV series. A spacecraft is launched towards another planetary system or nearby star in a journey that could literally take dozens or hundreds of years. Many generations will live and die aboard the ship until the star or planetary system is reached.
This would be a way in which the human race could eventually outlive their mother star, the Sun, and perpetuate its existence in the Universe.
| ADVANTAGES | DISADVANTAGES |
| Real exploration of deep space : By eventually building a starship and setting out for the stars, the human race will have met its ultimate challenge : exploring and colonizing deep space. | Crew selection : It would be very difficult to find human beings willing to spend their entire lives aboard a spaceship in order for their sons or grandsons to travel to the stars. Whole families should be sent aboard the ship in order to ensure t |
| Out from the Sun : Although it will happen in millions of years, the Sun as a star will eventually die and in the process end all life on Earth. A starship could be the first step in trying to escape the Earth�s inevitable end. | Technology : A self sufficient spacecraft en route to the stars would be very difficult to engineer with today�s technology. The space colony would have to be self sufficient and rely on accumulated energy when the Sun�s influence is no longer importa |
| Obsolescence : even if the starship could be built with today�s technology, in a voyage of several dozen years it could be overtaken halfway by a newer craft engineered many years later with advanced propulsion system. |
In order to select the most appropriate location for the space colony a reconsideration of the primordial objectives of building the Space Settlement becomes essential.
Although it is in man�s nature to explore and conquer, we must remember that the main reason for going out into space is a rational utilization of the Sun�s energy. At this stage in human evolution, our fate is still bound to the Sun and so it is scientifically rational to privilege energy considerations above the rest.
An analysis of the advantages and disadvantages of all the formulated alternatives yields immediate conclusions referred to each of them.
Low Earth Orbit doesn�t seem to be a good option. LEO has been exhaustively explored and it does not offer full access to solar energy. Besides, placing and keeping a mammoth spacecraft in LEO is entails an element of danger.
Geostationary and geosynchronous orbits offer several advantages, but the geostat region is clustered with communication satellites. It would also be too close to the Earth to really constitute deep space exploration. Energy requirements are practically the same as for greater distances.
Lunar Orbit is far from Earth, but presents the fundamental problem of not being permanently exposed to sunshine.
The gravity assist trajectories appear to interesting options, but varying conditions present to much of a technical challenge for an immature technology.
Finally, the starship concept is undoubtedly appealing, but again it would be very difficult to engineer. Crew selection limitations becomes a major drawback in that case.
The best option is, then, placing the space colony in a reduced orbit around any of the two libration points in the Moon�s orbit.
Permanent exposure to the Sun is granted, it is at enough distance from Earth to be considered deep space but not so far away as to make communications and remote operations impossible and its gravitational stability allow for relatively easy station keeping.
We have to bear in mind that the building and operation of space colonies is an untested, not mature technology and so any of the options that imply total disconnection from Earth can be considered for the future. The most logical first step would be to place the colony at one of the two mentioned libration points.
The Earth reminded us of a Christmas tree ornament hanging in the blackness of space. As we got farther and farther away it diminished in size. Finally it shrank to the size of a marble, the most beautiful marble you can imagine. That beautiful, warm, living object looked so fragile, so delicate, that if you touched it with a finger it would crumble and fall apart. Seeing this has to change a man, has to make a man appreciate the creation of God and the love of God. - James Irwin, US astronaut
Comments and suggestions : [email protected]
 NAS contact: Al Globus
NAS contact: Al Globus
|
Curator: Al Globus If you find any errors on this page contact Al Globus. |
 |
This site was hosted by the NASA Ames Research Center from 1994-2018 and is now hosted by:
